Warum Noten nicht normalverteilt sein sollten
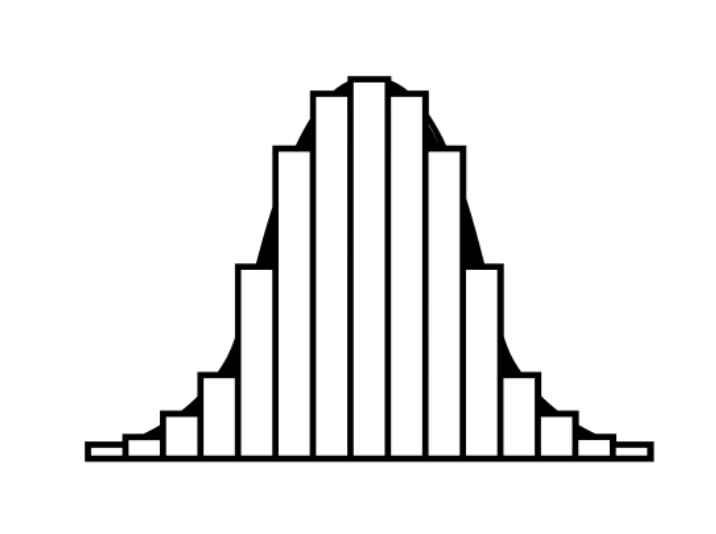
So sieht eine Normalverteilung aus. Die Verteilung beschreibt eine zufällige Streuung von Messwerten – wenn wir z.B. das Gewicht von neugeborenen Kätzchen messen würden, ergäbe sich bei einer großen Zahl von Messwerten eine Normalverteilung.
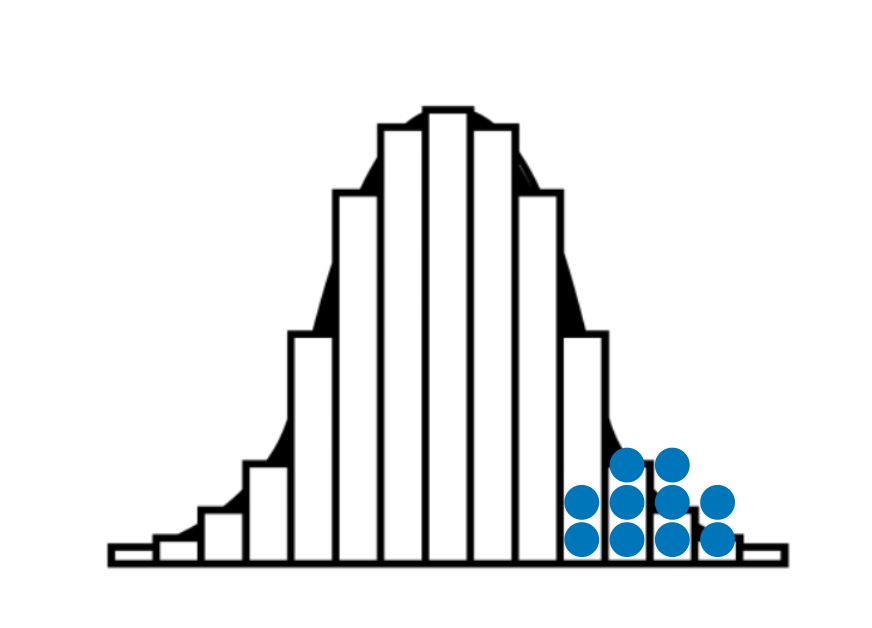
Viele Menschen denken, dass Noten auch einer Normalverteilung entsprechen sollten. Das hängt mit der Vorstellung zusammen, dass Noten als Messwerte betrachtet werden (was sie meiner Ansicht nach nicht sind). Daraus resultiert dann die Vorstellung, dass Noten ungefähr so aussehen sollten (ich gehe von einer Klasse mit 10 Schüler:innen aus, die roten Punkte sind ihre Noten):
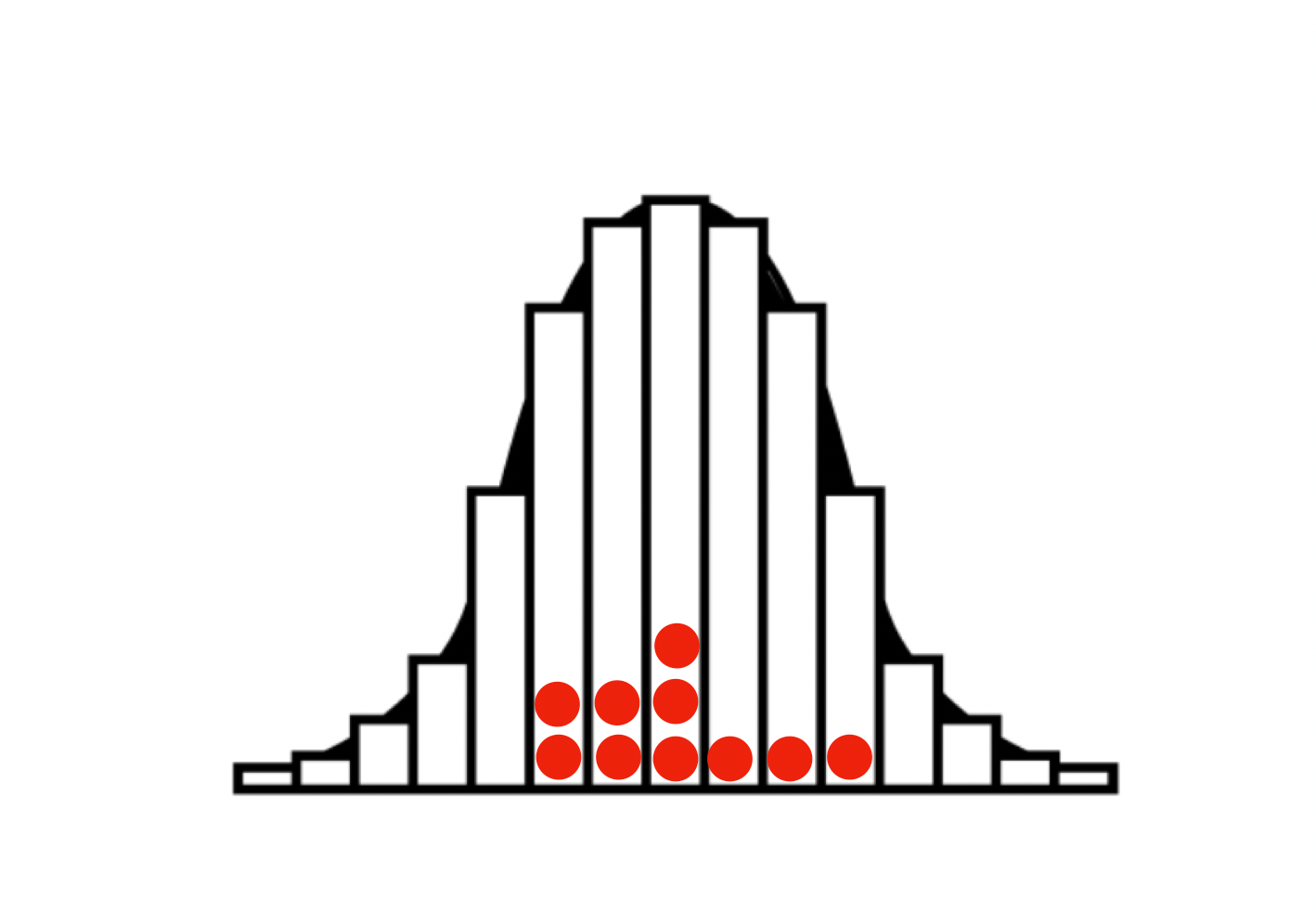
Diese Streuung entspricht ungefähr der Struktur der Normalverteilung. Die meisten Werte liegen in der Nähe vom Erwartungswert (das ist vereinfacht gesagt das arithmetische Mittel der Noten).
Diese Denkweise hat zwei grundsätzliche Probleme. Vor zwei Wochen habe ich den Mathematikdidaktiker Fischer zitiert, der geschrieben hat:
Für eine Klasse eine Normalverteilung der Noten (Leistungen) vorauszusetzen oder formal in den Bewertungen zu erzwingen, ist statistischer Unsinn.
Dafür gibt es drei Gründe:
- Noten sind keine Messwerte.
- Die Zahl von Schüler:innen in einer Klasse ist zu klein, damit der statistische Effekt eintritt.
- Da Noten Lernerfolge abbilden, sollte gar keine Normalverteilung sichtbar sein.
Den ersten Grund führe ich nicht weiter aus. Zum zweiten kann man sich überlegen, was passiert, wenn man die Würfe von 6 eher schweren Katzen auswertet: Die Wahrscheinlichkeit ist dann groß, dass die 24 geborenen Katzenjungen auch eher schwer sind und nicht der Normalverteilung entsprechen, die sichtbar würde, wenn wir die Würfe von 1000 Katzen auswerten würden.
Dasselbe gilt für eine Schulklasse. Ihre Noten können so aussehen:
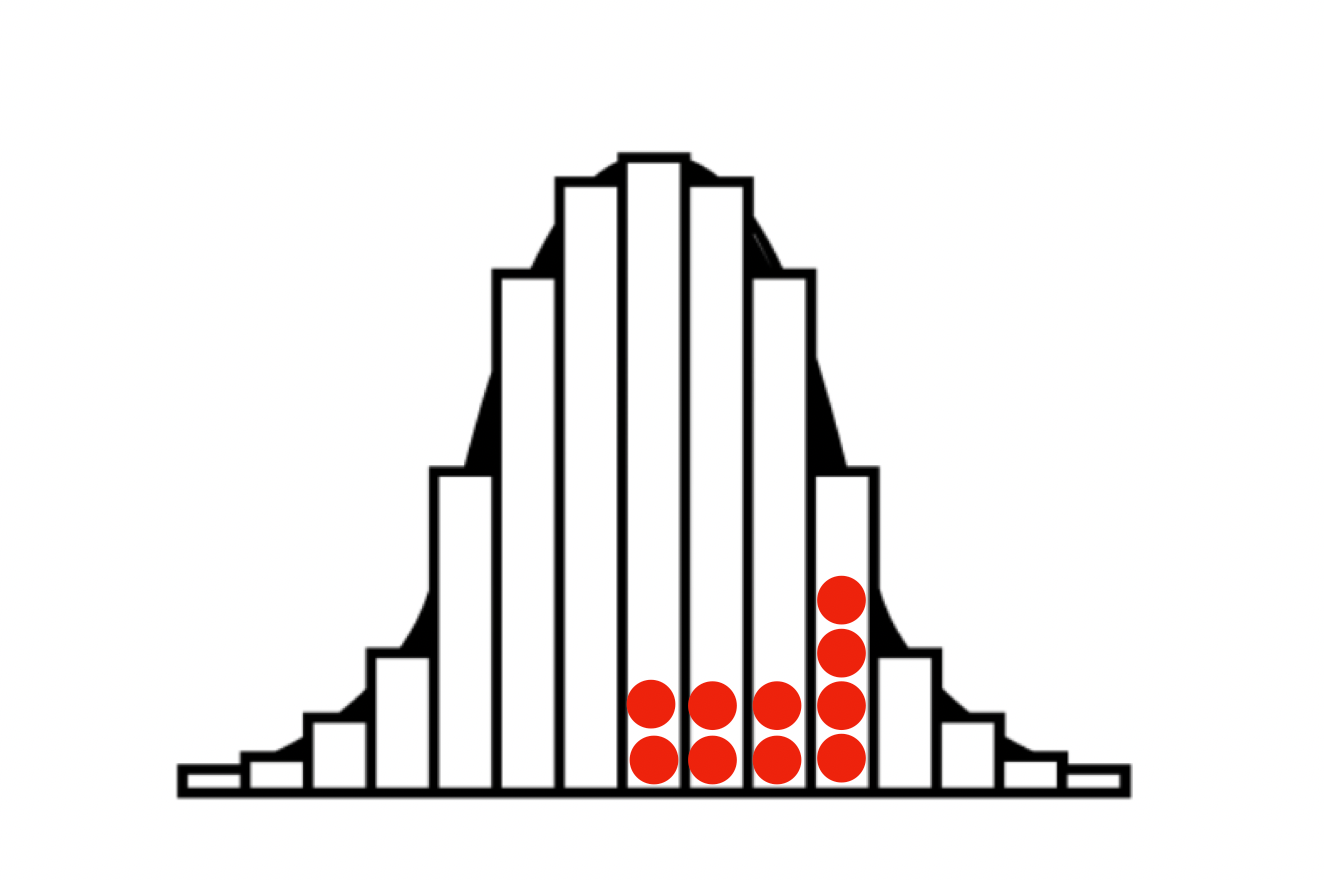
Oder auch so:
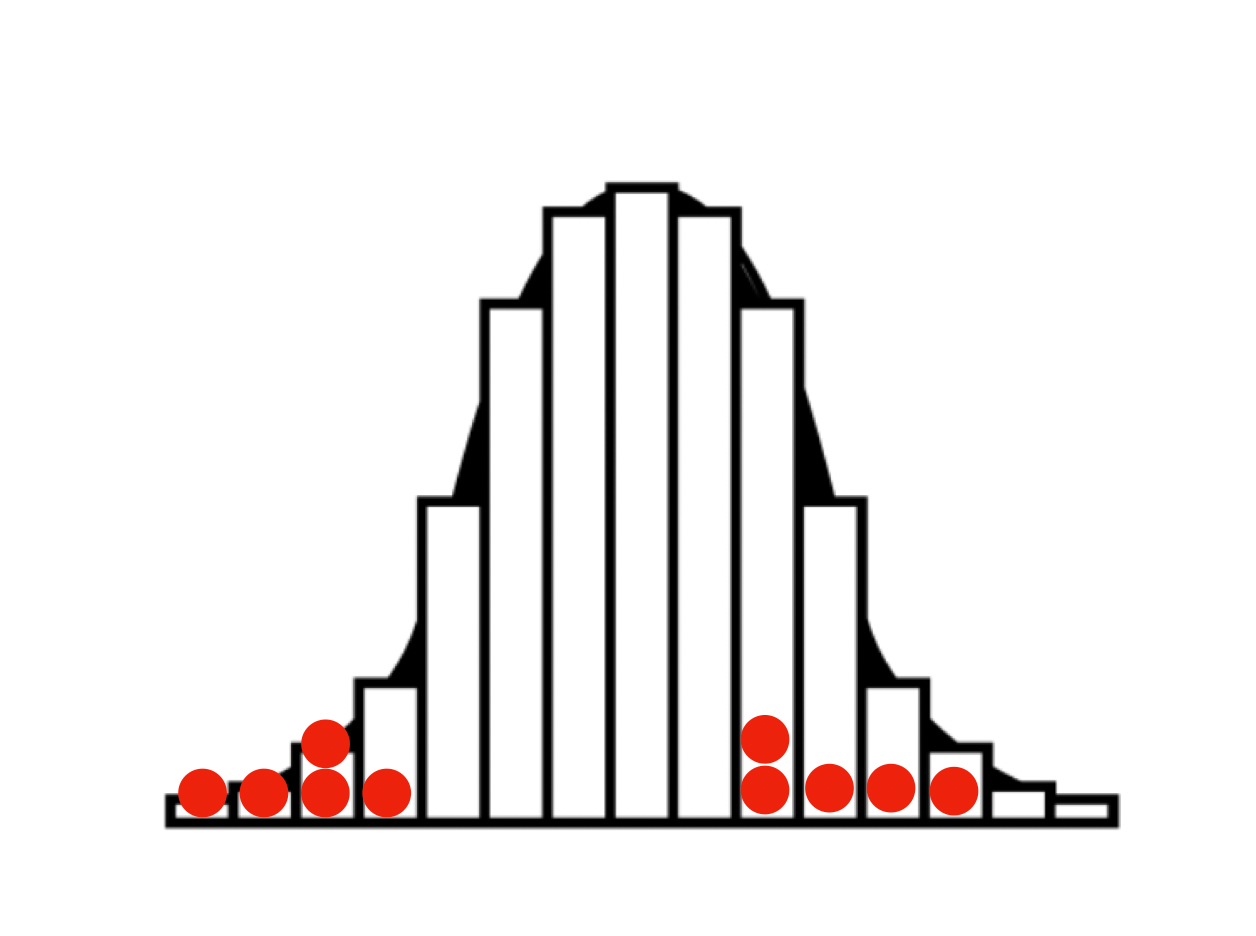
Das ist alles überhaupt nicht erstaunlich, sogar statistisch zu erwarten (seltsam wäre, wenn es in jeder Klasse eine Normalverteilung gäbe).
Das führt zu einem Zwischenfazit: Wenn Lehrpersonen darauf achten, dass ihre Noten eine Normalverteilung ergeben, dann verzerren sie die Noten so, dass sich gar nicht mehr das abbilden, was sie abbilden sollten.
Damit kommen wir zum dritten Problem. Benjamin Bloom hat 1968 einen Aufsatz mit dem Titel Learning for Mastery geschrieben. Darin findet sich eine prägnante Kritik an der Idee der Normalverteilung:
The normal curve is a distribution most appropriate to chance and random activity. Education is a purposeful activity and we seek to have students learn what we would teach. Therefore, if we are effective, the distribution of grades will be anything but a normal curve. In fact, a normal curve is evidence of our failure to teach. […]
If we are effective in our instruction, the distribution of achievement should be very different from the normal curve. In fact, we may even insist that our educational efforts have been unsuccessful to the extent that the distribution of achievement approximates the normal distribution.
(Bloom 1968, S. 2)
Wenn Lehrpersonen also mit Schüler:innen zusammen Lernziele erreichen, dann sollten alle gute Noten haben. Die Verteilung sollte also ungefähr so aussehen:
In ihrer Einleitung zum Buch Ungrading schreibt Susan D. Blum, Normalverteilung sei keine Beschreibung von Noten, sondern eine Behauptung, die aus einer falschen Analogie entstünde: Einerseits gibt es menschliche Merkmale, die normalverteilt sind (die Körpergröße zum Beispiel), andererseits werden bestimmte Tests (IQ-Test) so gestaltet, dass sie einer Normalverteilung entsprechen (ein IQ von 100 entspricht dem Erwartungswert oder Durchschnitt – es handelt sich also erstens um den Wert, der den meisten Menschen zugeteilt wird und zweitens um den Wert, der die Grenze zwischen über- und unterdurchschnittlich intelligenten Menschen markiert). Blum hält abschließend fest:
But the belief that this [die Normalverteilung] applies to human learning is a claim and an assertion, not a finding.
